W niektórych źródłach mówi się o znaczeniu kolejności stosowania przechyłu, pochylenia i odchylenia. Ale nie mogę zrozumieć, dlaczego jest to powiązane.
Weź prawą rękę: skieruj kciuk w górę, palec wskazujący od siebie, a środkowy w lewo. Masz teraz praworęczny układ współrzędnych: kciuk to oś x, palec wskazujący to oś y, a środkowy - oś z.
Najpierw obróć + 90 ° wokół osi x (kciuk). Twój palec wskazujący wskazuje teraz w lewo, a środkowy palec na Ciebie. Następnie obróć o + 90 ° wokół osi y (palec wskazujący). Twój kciuk jest teraz skierowany od Ciebie, palec wskazujący w lewo, a palec środkowy w górę.
Teraz wróć do pozycji wyjściowej i wykonaj te same dwa obroty w innej kolejności, najpierw wokół oś y, a następnie oś x: Obróć o + 90 ° wokół osi y (palec wskazujący). Twój kciuk jest teraz skierowany w prawo, palec wskazujący z dala od Ciebie, a palec środkowy w górę. Następnie obróć o + 90 ° wokół osi X (kciuk). Twój kciuk jest teraz skierowany w prawo, palec wskazujący w górę, a palec środkowy w Twoją stronę.
Różni się to od ostatniego wyniku: kolejność obrotu ma znaczenie.
Użyłem wartości akcelerometru, wprowadzając je do pewnych formuł w Internecie (te wzory arcus tangens, których wszyscy używają, ale nikt dobrze ich nie wyjaśnia)
Gdy samolot porusza się ze stałą prędkością, akcelerometr mierzy tylko przyspieszenie ziemskie, które jest wektorem skierowanym dokładnie w dół (0, 0, -g) w globalnym układzie współrzędnych. Jest to zawsze prawdziwe, niezależnie od orientacji czujnika.
Jeśli czujnik jest idealnie wypoziomowany, lokalny układ współrzędnych czujnika jest wyrównany z globalnym układem współrzędnych, więc czujnik mierzy również (0, 0, -g).
Kiedy czujnik jest nachylony, mierzony wektor również ma składowe xiy.
Aby uprościć sprawę, wyobraź sobie przypadek, w którym czujnik jest przechylony wokół dodatniej osi y.
Czujnik mierzy teraz składową x oraz składową az: (x, 0, -z).
Jak widać na poniższym obrazku, kąt obrotu θ = atan2 (x, z) .
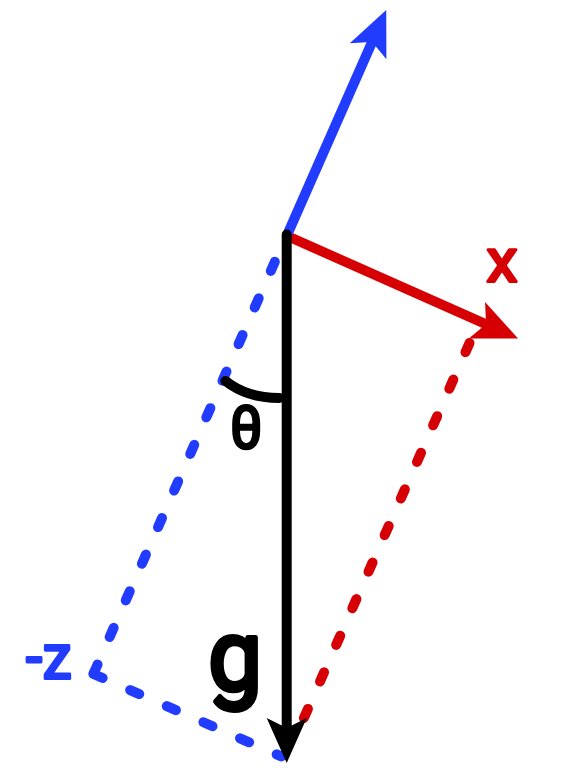Czarna strzałka to przyspieszenie ziemskie, a czerwona i niebieska strzałka to osie x i z układu współrzędnych czujnika (pochylonego).
Jednak pomiary akcelerometru nie są przydatne do określania orientacji, gdy czujnik przyspiesza, ponieważ wtedy mierzony wektor nie wskazuje już dokładnie w dół (w globalnym układzie współrzędnych).
Żyroskopy mierzą prędkość kątową. Całkując prędkość kątową, otrzymujesz kąt.
Jest jedno zastrzeżenie: nie można przeprowadzić dokładnej całkowania, ponieważ mamy pomiary tylko w dyskretnych punktach w czasie. Oznacza to, że musimy użyć czegoś w rodzaju metody Eulera, o której wiadomo, że powoduje dryf oszacowania orientacji. Co gorsza, pomiar jest zaszumiony, a szum ten jest również zintegrowany, co skutkuje jeszcze większym błędem.
Na szczęście można połączyć oba niedoskonałe pomiary w jedną, lepszą ocenę orientacji za pomocą czujnika algorytm fuzji. Z powodzeniem zastosowałem algorytm Sebastiana Madgwicka dla mojego quadkoptera.
Wykorzystuje on pomiary akcelerometru, aby zminimalizować dryf żyroskopu.
Zauważ, że ten algorytm używa kwaternionów zamiast Eulera kąty (przechylenie, pochylenie, odchylenie), ponieważ te ostatnie cierpią na blokadę gimbala i ponieważ kwaternionie generalnie wymagają mniejszej mocy obliczeniowej.
Pamiętaj również, że nie możesz określić kąta odchylenia za pomocą akcelerometru, więc trochę dryfować na tym pomiarze.
Dobrze jest wykonywać wszystkie obliczenia przy użyciu kwaternionów. Prawdopodobnie nie będziesz potrzebować kątów Eulera dla swojego quadkoptera, może z wyjątkiem celów debugowania.
Jeśli chcesz, możesz również pobrać kwaternion bezpośrednio z wektora przyspieszenia:
Quaternion quaternionFromDirection (Vec3f v) {/ * * Wzór: * q = cos (ϑ / 2) + sin (ϑ / 2) · (x · i + y · j + z · k) * gdzie (xyz) jest wektorem jednostkowym reprezentującym oś, wokół której * ciało jest obrócony; ϑ to kąt, o który jest obracany. * * Źródło: * https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation#Using_quaternion_as_rotations * * Oś obrotu (x y z) można obliczyć, biorąc znormalizowany * iloczyn poprzeczny (0 0 1) i danego wektora. Kąt obrotu * ϑ można znaleźć za pomocą | A × B | = | A || B | · sin (ϑ). * / // Najpierw sprawdź przypadek krawędzi, gdzie v == (0 0 z), tj. Pionowo if (v.x == 0 && v.y == 0) return {1, 0, 0, 0}; // Oblicz iloczyn poprzeczny i jego normę. Vec3f cross = {v.y, -v.x, 0}; float crossNorm = cross.norm (); cross / = crossNorm; // Oblicz kąt ϑ. float angle = std :: asin (crossNorm / v.norm ()); // Oblicz wynikową kwaternion. return {std :: cos (angle / 2), // std :: sin (angle / 2) * cross.x, // std :: sin (angle / 2) * cross.y, // std :: sin (kąt / 2) * cross.z, //}; }